数据结构中关于图的知识。

图的基本知识

图的类型

三个类型：

1. 无向图
2. 有向图
3. 加权图

无向图

无向图中任意两个顶点之间的边都是没有方向的。

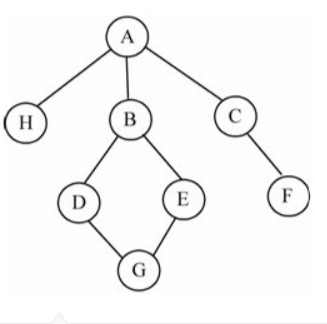
有向图

有向图中任意两个顶点之间的边都是有方向的。

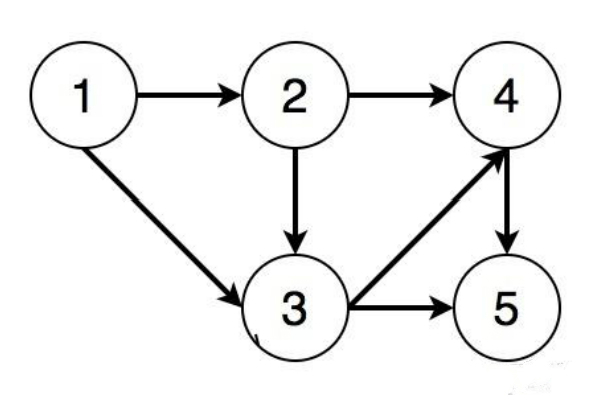
加权图

加权图中的每条边都带有一个相关的权重。这里的权重可以是任何一种度量。

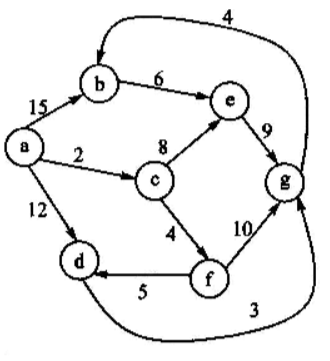
图的定义

图是由顶点和边组成的一种非线形数据结构。

图的相关术语

• 顶点：边的交点均称为「图」的顶点。
• 边：顶点之间的连接线称为边。
• 路径：从一个顶点到另一个顶点之间经过的所有顶点的集合。
  注意：两个顶点之间的路径可以是很多条。
• 路径长度：一条路径上经过的边的数量。
• 环：起点和终点为同一个顶点的路径。
• 负权环：在 加权图 中，如果一个环的所有边的权重加起来为负数，我们就称之为 负权环 。
• 连通性：两个不同顶点之间存在至少一条路径，则称这两个顶点是连通的。
• 顶点的度： 度 适用于无向图，指的是和该顶点相连接的所有边数称为顶点的度。
• 顶点的入度： 入度 适用于有向图，一个顶点的入度为n，则表示有n条与顶点相连的边指向该顶点。
• 顶点的出度： 出度 适用于有向图，它与「入度」相反。一个顶点的出度为n，则表示有n条与顶点相连的边以该顶点为起点。

并查集

并查集的作用

「并查集」的主要作用是用来解决网络中的连通性。

并查集的常用术语

• 父节点：顶点的直接父亲节点。
• 根节点：没有父节点的节点，本身可以视为自己的父节点。

并查集的基本思想

并查集的编程思想

并查集的两个重要函数

Quick Find 实现方式：找到给定顶点的根结点。

Quick Union 实现方式：合并两个顶点，并将他们的根结点保持一致。。

「并查集」的两个实现方式

Quick Find 实现方式：它指的是实现「并查集」时，find 函数时间复杂度很低为 O(1)，但对应的 union 函数就需要承担更多的责任，它的时间复杂度为 O(N)。

Quick Union 实现方式：它指的是实现「并查集」时，相对于 Quick Find 的实现方式，我们通过降低 union 函数的职责来提高它的效率，但同时，我们也增加了 find 函数的职责。

Quick Find 的「并查集」

代码实现

// UnionFind.class
public class UnionFind {
    int root[];

    public UnionFind(int size) {
        root = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
        }
    }

    public int find(int x) {
        return root[x];
    }
		
    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            for (int i = 0; i < root.length; i++) {
                if (root[i] == rootY) {
                    root[i] = rootX;
                }
            }
        }
    };

    public boolean connected(int x, int y) {
        return find(x) == find(y);
    }
}

// App.java
// 测试样例
public class App {
    public static void main(String[] args) throws Exception {
        UnionFind uf = new UnionFind(10);
        // 1-2-5-6-7 3-8-9 4
        uf.union(1, 2);
        uf.union(2, 5);
        uf.union(5, 6);
        uf.union(6, 7);
        uf.union(3, 8);
        uf.union(8, 9);
        System.out.println(uf.connected(1, 5)); // true
        System.out.println(uf.connected(5, 7)); // true
        System.out.println(uf.connected(4, 9)); // false
        // 1-2-5-6-7 3-8-9-4
        uf.union(9, 4);
        System.out.println(uf.connected(4, 9)); // true
    }
}

参考

作者：爱学习的饲养员

链接：https://leetcode-cn.com/leetbook/read/graph/r340gv/

来源：力扣（LeetCode）

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。