二分查找的分析，这个方法真是太好用了，感谢这个B~站大佬。

二分法

通用步骤

分析

将二分法的处理过程划分成左右两个区域的 动态变化 的过程。当Left和Right 相差唯一时，结束循环，提交结果。

划归

将问题划归为左右两个区域的动态变化问题，最后提交一个L/R的值。

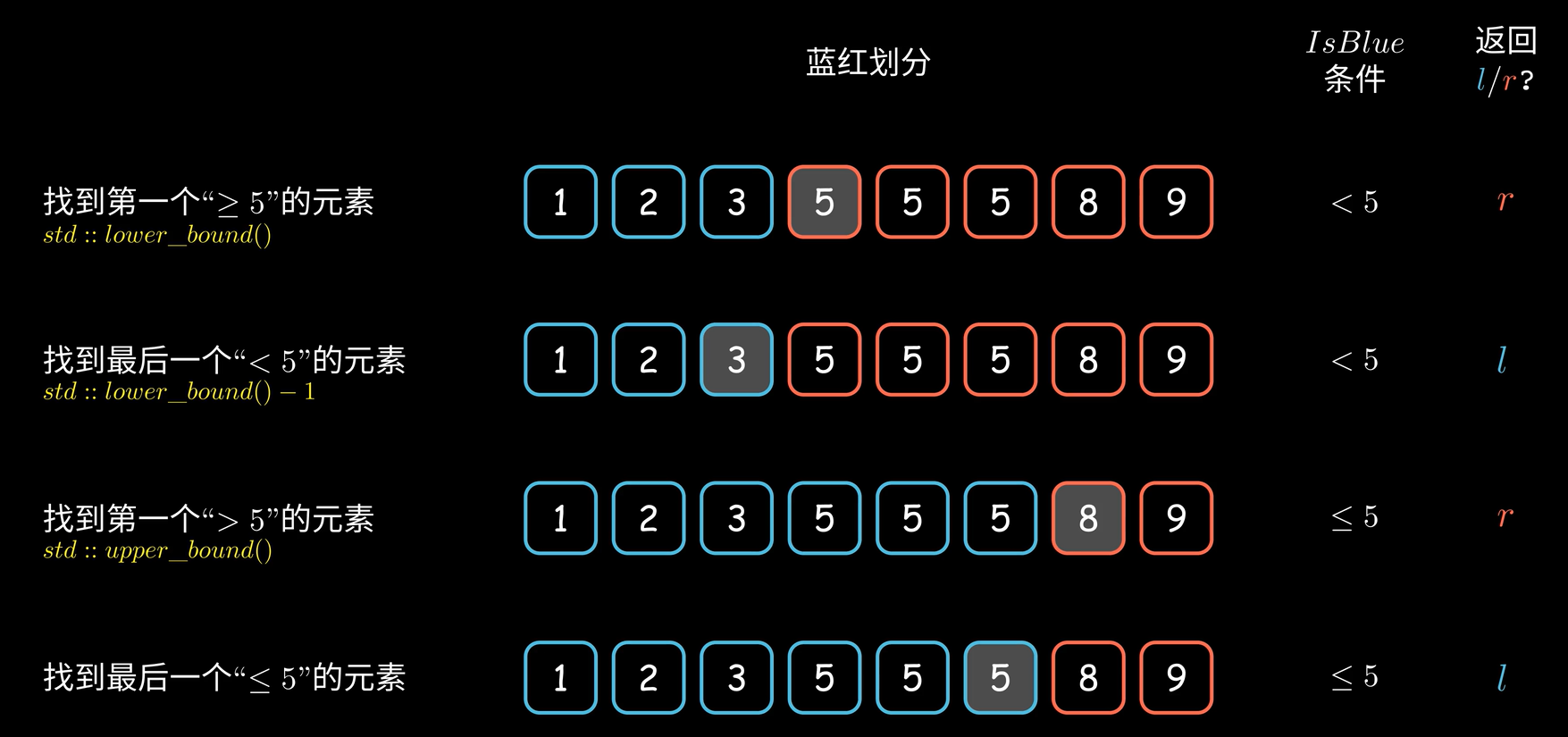
套路

public int searchInsert(int[] nums, int target) {
    int left = -1;//左边界-1
    int right = nums.length;//右边界+1
    int middle = (left + right) / 2;//中间值
    while(left + 1 != right){  //L和R相差1时，结束
        //分析与划归片段，需要自行分析
        if (middle == nums[middle]){
            return middle;
        } else if (target > nums[middle]){
            left = middle;
        }else{
            right = middle;
        }
        //-----------------
        middle = left + (right - left)/2;////重新定位去中间值指针
    }
    return right;//分析与划归分析，确定返回L或R
}

注意问题

m是否始终处于[0, N)以内?

始终处于区间内。

更新指针时，能不能写成l=m+1,或者r=m- 1?

不能，在这个方法里，会冲突，溢出。

题目

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。

分析

方法：二分查找
二分查找是一种基于比较目标值和数组中间元素的教科书式算法。

• 如果目标值等于中间元素，则找到目标值。
• 如果目标值较小，继续在左侧搜索。
• 如果目标值较大，则继续在右侧搜索。

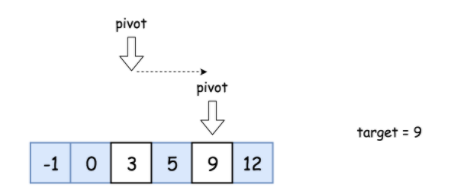
算法：

class Solution {
  public int search(int[] nums, int target) {
    int pivot, left = 0, right = nums.length - 1;//初始化指针 left = 0, right = n - 1。
    while (left <= right) {//当 left <= right：
      pivot = left + (right - left) / 2;
      if (nums[pivot] == target) return pivot;
      if (target < nums[pivot]) right = pivot - 1;
      else left = pivot + 1;
    }
    return -1;
  }
}

复杂度分析

• 时间复杂度：\mathcal{O}(\log N)O(logN)。
• 空间复杂度：\mathcal{O}(1)O(1)。

易错

if (target < nums[pivot]) right = pivot - 1;
else left = pivot + 1;

左右多移动一格，可以避免，不存在列表的数字，在游标函数相差为1的时候进入死循环。

参考

作者：LeetCode

链接：https://leetcode-cn.com/problems/binary-search/solution/er-fen-cha-zhao-by-leetcode/

来源：力扣（LeetCode）

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

二分查找为什么总是写错？